Lattice of subgroups
In mathematics, the lattice of subgroups of a group 
is the lattice whose elements are the subgroups of , with the partial order relation being set inclusion. In this lattice, the join of two subgroups is the subgroup generated by their union, and the meet of two subgroups is their intersection.
Lattice theoretic information about the lattice of subgroups can sometimes be used to infer information about the original group, an idea that goes back to the work of Øystein Ore (1937, 1938). For instance, as Ore proved, a group is locally cyclic if and only if its lattice of subgroups is distributive. Lattice-theoretic characterizations of this type also exist for solvable groups and perfect groups (Suzuki 1951).
Contents |
Example
The dihedral group Dih4 has ten subgroups, counting itself and the trivial subgroup. Five of the eight group elements generate subgroups of order two, and two others generate the same cyclic group C4. In addition, there are two groups of the form C2×C2, generated by pairs of order-two elements. The lattice formed by these ten subgroups is shown in the illustration.
Characteristic lattices
Subgroups with certain properties form lattices, but other properties do not.
- Nilpotent normal subgroups form a lattice, which is (part of) the content of Fitting's theorem.
- In general, for any Fitting class F, both the subnormal F-subgroups and the normal F-subgroups form lattices. This includes the above with F the class of nilpotent groups, as well as other examples such as F the class of solvable groups. A class of groups is called a Fitting class if it is closed under isomorphism, subnormal subgroups, and products of subnormal subgroups.
- Central subgroups form a lattice.
However, neither finite subgroups nor torsion subgroups form a lattice: for instance, the free product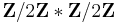 
is generated by two torsion elements, but is infinite and contains elements of infinite order.
See also
- Zassenhaus lemma, an isomorphism between certain quotients in the lattice of subgroups
- Complemented group, a group with a complemented lattice of subgroups
- Lattice theorem, a Galois connection between the lattice of subgroups of a group and of its quotient
- Example: Lattice of subgroups of the symmetric group S4
References
- Baer, Reinhold; Hausdorff, Felix (1939). "The significance of the system of subgroups for the structure of the group". American Journal of Mathematics (The Johns Hopkins University Press) 61 (1): 1–44. doi:10.2307/2371383. JSTOR 2371383.
- Ore, Øystein (1937). "Structures and group theory. I". Duke Mathematical Journal 3 (2): 149–174. doi:10.1215/S0012-7094-37-00311-9. MR1545977.
- Ore, Øystein (1938). "Structures and group theory. II". Duke Mathematical Journal 4 (2): 247–269. doi:10.1215/S0012-7094-38-00419-3. MR1546048.
- Rottlaender, Ada (1928). "Nachweis der Existenz nicht-isomorpher Gruppen von gleicher Situation der Untergruppen". Mathematische Zeitschrift 28 (1): 641–653. doi:10.1007/BF01181188.
- Schmidt, Roland (1994). Subgroup Lattices of Groups. Expositions in Math. 14. Walter de Gruyter. ISBN 9783110112139. Review by Ralph Freese in Bull. AMS 33 (4): 487–492.
- Suzuki, Michio (1951). "On the lattice of subgroups of finite groups". Transactions of the American Mathematical Society (American Mathematical Society) 70 (2): 345–371. doi:10.2307/1990375. JSTOR 1990375.
- Suzuki, Michio (1956). Structure of a Group and the Structure of its Lattice of Subgroups. Berlin: Springer Verlag.
- Yakovlev, B. V. (1974). "Conditions under which a lattice is isomorphic to a lattice of subgroups of a group". Algebra and Logic 13 (6): 400–412. doi:10.1007/BF01462952.